코인포커 투명 카드 셔플링에 대한 고급 분석 가이드

기존의 온라인 포커룸은 카드 셔플링 소프트웨어를 공개하지 않아, 플레이어들은 카드가 공정하게 섞이고 있는지 확인할 방법이 없었습니다. 하지만 이제는 다릅니다! 코인포커의 투명한 카드 셔플러는 바로 이 문제를 해결하기 위해 탄생했습니다.

이 시스템은 한 방향 암호학적 해시 함수를 활용하여 셔플링 과정을 안전하게 공개하며, 이를 통해 플레이어는 다음을 직접 확인할 수 있습니다.

• 핸드 하인드사이트(Hand Hindsight) 를 이용한 딜링 되지 않은 카드 확인
• RNG 검증 도구(RNG Validation Tool)를 통한 개인기여 데이터 검증
• RNG(Random Number Generator) 작동 원리의 투명한 확인

투명한 카드 셔플링 기술을 깊이 살펴보기 전에, 간단한 튜토리얼로 직접 테스트해 보세요!

검증 도구를 활용해 내 참여를 증명하는 방법

코인포커의 투명한 카드 셔플러가 처음이라면, 먼저 스크린샷이 포함된 기본 가이드를 확인해 보세요!

1단계: 핸드가 공정하게 진행되었는지 확인하려면 한 방향 해시 함수 데이터를 살펴봐야 합니다. 이를 확인하려면 핸드 히스토리 탭 하단의 RNG Shuffle Order 링크를 클릭하세요.

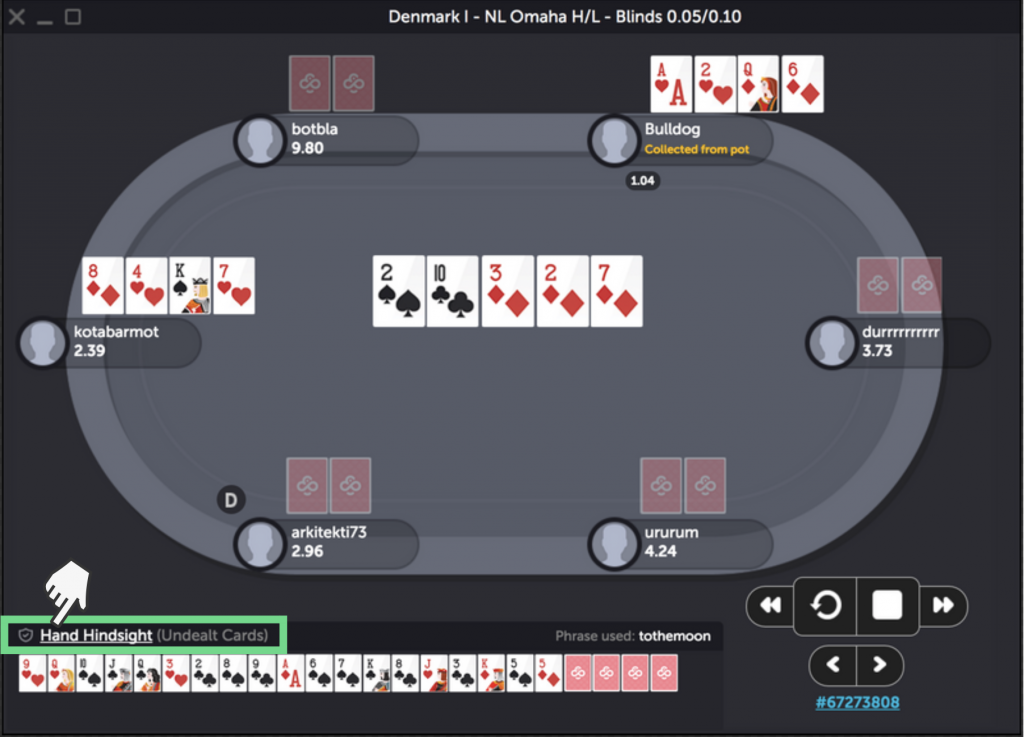
2단계: 여기서 긴 해시값 목록을 확인할 수 있습니다. 목록에는 다음 정보가 포함됩니다.

• 초기 덱 순서에 따른 카드별 해시값
• 각 플레이어와 코인포커가 제출한 암호화된 시드 값
• 최종 덱 순서에 따른 카드 해시값

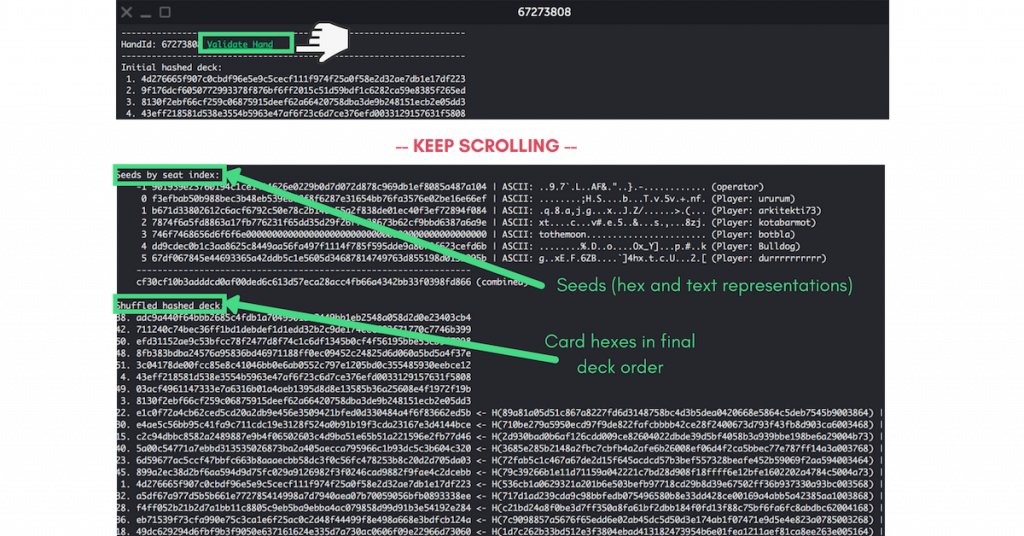
여기서 셔플된 해시 덱 아래에 나열된 숫자는 덱 내 카드의 위치를 나타내며, 플레이어 해시값은 핸드 시작 시 제출된 개별 암호화 값(즉, ‘셔플링 요소‘)입니다.

6단계: 이 데이터를 활용하려면 반드시 검증 도구(Validation Tool)가 필요합니다. 창 상단의 링크를 클릭하여 바로 확인해 보세요

7단계: 이제 핸드를 검증할 차례입니다. 방법은 두 가지가 있으며, 원하는 방식으로 진행할 수 있습니다.

1. 셔플 과정에 직접 참여했음을 증명
2. 최종 덱에서 특정 카드의 위치가 셔플 전 암호화된 위치와 일치하는지 검증

옵션 1: 셔플 참여 검증

‘셔플링 요소’ 또는 암호화된 시드를 검증 도구에 입력하세요. 이 시드는 파란색 화살표로 표시됩니다. 결과물은 ‘집합적 셔플링 요소(Collective shake factor)’ 또는 결합된 해시, 그리고 최종 덱 순서입니다.

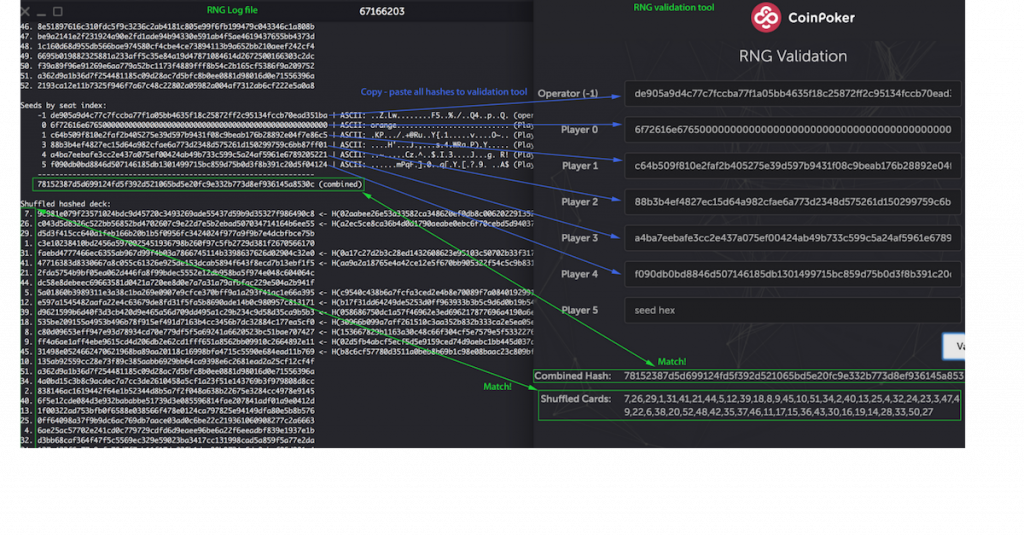
✅ 두 값이 일치하면, 셔플 과정에 참여한 것이 성공적으로 검증된 것입니다!

옵션 2: 개별 카드 검증

딜링 된 카드 중 하나를 선택하세요 (이 카드는 왼쪽에 해시값, 오른쪽에 암호화된 해시 함수가 표시됩니다). 오른쪽에 있는 함수 안에 해시값을 입력한 후, 카드 검증 섹션에서 결과를 확인하세요. 출력값은 코인포커에 표시된 왼쪽 해시 값과 올바른 카드 값이 될 것입니다.

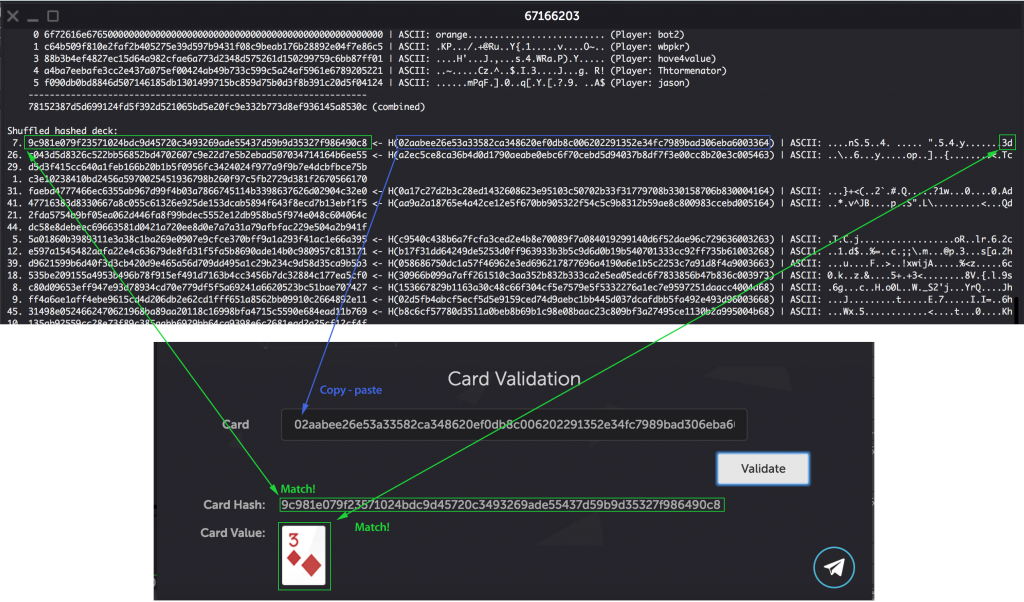
8단계: 딜링 되지 않은 카드도 확인하고, 코인포커의 완전히 새로운 탈중앙화 RNG 시스템을 직접 경험해 보세요!

---

자세한 설명: 코인포커의 RNG는 어떻게 작동할까?

먼저, 셔플되지 않은 카드 덱을 가정해 보겠습니다.: 2c, Qd, Kh

실제 게임에서는 하나의 덱에 52장의 카드가 있지만, 개념을 쉽게 이해하기 위해 3장만 사용해 설명하겠습니다. 이 초기 덱 순서를 기반으로, 코인포커는 다음 단계에 따라 모든 플레이어와 정보를 공유합니다.

1단계: RNG 시작

코인포커는 시드(Seed)를 기반으로 RNG(Random Number Generator; 난수 생성기)를 실행합니다. 이 값은 일시적으로만 존재하며, 난수 생성 과정의 초기 입력값으로 사용됩니다.

2단계: 카드 암호화 과정

코인포커는 난수 시드를 이용해 솔트(Salt) 값을 생성합니다. 이 솔트 값은 비밀번호 역할을 하는 랜덤 데이터이며, 각 카드와 결합해 한 방향 암호화 해시(Hash)를 생성합니다. 앞서 언급한 3장의 카드에 적용하면 다음과 같은 방식이 됩니다.:

• Hash(2c + salt1) = aa
• Hash(Qd + salt2) = bb
• Hash(Kh + salt3) = cc

※ 여기서 aa, bb, cc는 이해를 돕기 위해 단순화한 값이며, 실제 해시는 256비트의 복잡한 암호 문자열로 변환됩니다.

3단계: 덱 셔플

1단계에서 생성한 난수 시드를 사용하여 2단계에서 암호화한 카드 덱을 섞습니다.

• 셔플 전 (해싱된 덱): aa (2c), bb (Qd), cc (Kh)
• 셔플 후 (최종 덱): bb (Qd), cc (Kh), aa (2c)

4단계: 플레이어들에게 해싱된 덱 공유

코인포커는 초기 덱 순서의 모든 카드 해시값을 포함하는 암호화된 덱(벡터 형태)을 각 플레이어에게 전송합니다.

이렇게 하는 이유는 특정 카드는 공개할 수 있도록 하면서도, 폴드된 핸드처럼 숨겨야 할 카드는 여전히 비공개로 유지할 수 있도록 하기 때문입니다. 이제 모든 플레이어는 초기 덱 순서를 해시 형태로 확인할 수 있습니다.

다음 단계에서는 플레이어들의 입력을 반영하여 초기 덱을 최종 덱으로 변환하는 과정을 설명합니다.
코인포커와 플레이어들의 입력이 결합되어 최종적으로 집합적 시드(aggregate seed)가 생성됩니다.

5단계: 예시

이해하기 쉽게, 두 명의 플레이어가 있다고 가정해 보겠습니다. 이들의 이름을 유진과 민수라고 하겠습니다.

6단계: 플레이어의 입력 반영

유진과 민수는 자신의 시드(seed)를 해싱하여 코인포커에 제출해야 합니다. 이 과정은 다음과 같습니다.:

• Hash(유진의_시드) = XX
• Hash(민수의_시드)  = YY

7단계: 새로운 무작위 시드 생성

코인포커는 1단계와는 다른 새로운 시드를 생성하고, 이를 해싱합니다.

Hash(코인포커의_시드) = ZZ

8단계: 기여 시드 리스트 구성

이제 플레이어들의 시드와 코인포커의 시드를 조합하여 기여 시드(commitment seeds) 리스트를 생성합니다.

[XX, YY, ZZ]

9단계: 기여 시드 공유

코인포커는 이 리스트를 유진과 민수에게 공유합니다.

10단계: 실제 시드 제출 및 검증

유진와 민수은 5단계에서 사용했던 원래 시드를 제출합니다.

Hash(유진의_시드) = XX  
Hash(민수의_시드) = YY

11단계: 집합적 시드 생성

이제 플레이어들과 코인포커의 시드를 하나로 합쳐 집합적 시드(aggregated seed)를 생성합니다.

Hash(유진의_시드 + 민수의_시드 + 코인포커의_시드) = 집합적_시드 

12단계: 최종 덱 확정

이제 코인포커는 집합적 시드를 이용해 최종 덱을 셔플합니다. 그 후, 최종 덱의 해시값을 모든 플레이어에게 공유합니다.

초기 덱: Qd, Kh, 2c →  RNG(집합적_시드 적용) → 최종 덱: Kh, 2c, Qd
              (해시: cc, aa, bb)

이제 이 덱이 핸드가 종료될 때까지 사용됩니다.

RNG 검증 도구의 작동 방식

암호화 해시 함수를 사용하면 셔플 과정의 일부 정보를 안전하게 공개할 수 있으며, 이를 활용하면 게임이 공정하게 진행되었는지 검증할 수 있습니다. 이 기능을 제공하는 것이 바로 RNG 검증 도구(Validation Tool)입니다.

유진과 민수는 서로의 실제 시드를 알 수 없고, 자신의 시드만 확인할 수 있습니다. 하지만 8~9단계에서 설명한 대로, 모든 플레이어와 코인포커의 시드 해시값에는 접근할 수 있습니다.

핸드 종료 후, 각 플레이어는 모든 참가자의 실제 시드를 확인할 수 있으며, 이를 이용해 최종 덱 셔플이 공정하게 이루어졌는지 검증할 수 있습니다.

13~18단계: 셔플된 덱에 대한 플레이어의 영향 검증

13단계: 시드 반영 확인

먼저, 각자의 실제 시드를 사용해 받은 해시값이 올바른지 검증해야 합니다. 즉, 해당 시드를 해시 함수에 넣었을 때 원래 받았던 값과 동일한지 확인하는 과정입니다.

예: Hash(유진의_시드) = XX 가 성립하면, 검증 완료

14단계: 최종 집계된 시드 검증

모든 플레이어와 코인포커의 실제 시드가 확인되면, 집합적 시드도 검증할 수 있습니다. 이를 위해, 각 플레이어와 서버의 실제 시드를 모두 더한 후, 해시 함수에 넣어 결과를 비교하면 됩니다.

Hash(유진의_시드 + 민수의_시드 + 서버_시드) = 집합적 시드

15단계: 최종 덱 셔플 과정 검증

집계된 시드가 정확하게 확인되면, 이제 유진이나 민수는 최종 덱 해시와 집계된 시드를 사용해 초기 덱을 다시 계산할 수 있습니다. 즉, 이전 단계에서 받았던 초기 덱과 일치하는지 확인하는 과정입니다.

16단계: 셔플 과정 참여 증명

만약 결과가 초기 덱 해시 순서와 동일하다면, 이제 플레이어는 최종 덱 셔플 과정에 직접 참여했음을 확인할 수 있습니다.

하지만 여기서 끝이 아닙니다!
플레이어는 셔플이 공정하게 이루어졌는지, 즉 카드 순서가 정말 무작위였는지도 검증할 수 있습니다. 이 검증은 커뮤니티 카드 및 공개된 핸드에 대해서만 가능하며, (먹 핸드는 검증 불가) 설명을 돕기 위해 첫 두 장의 카드를 예시로 들겠습니다.

17단계: 딜링된 카드의 무작위성 검증

핸드가 종료된 후, 플레이어는 모든 실제 시드와 함께, 첫 두 장의 카드 값과 해당 salt 값을 받습니다. 카드값과 salt는 2단계에서 해시 계산에 사용된 값입니다.

예: Hash(Kh + salt3) = cc

18단계: 최종 덱 셔플 확인

이제 유진과 민수는 모든 변숫값을 알게 되었으므로, 이를 이용해 해시 함수를 역산하여 최종 덱을 검증할 수 있습니다.

즉, Hash(Kh + salt3)을 계산했을 때 cc가 나오면, 해당 카드(Kh)가 최종 덱의 첫 번째 카드였음이 증명됩니다.

✅ 이 방법은 모든 공개된 카드에 대해 적용할 수 있습니다.
❌ 하지만 먹 핸드(버려진 카드)나 딜링 되지 않은 카드는 salt 값을 받을 수 없기 때문에, 이 방법으로 검증할 수 없습니다.

전문가 설명

위의 설명은 일반 포커 플레이어에게는 복잡한 정보일 수 있지만, 암호학에 관심 있는 사람들에게는 그저 빙산의 일각에 지나지 않습니다. 아래 링크에서 GitHub의 오픈 소스 코드를 확인할 수 있습니다:

• GitHub 투명한 RNG 오픈 소스 코드